Industry Article
Multidimensional simultaneous random plus erratic noise attenuation and interpolation for seismic data by Joint Low-Rank and Sparse Inversion
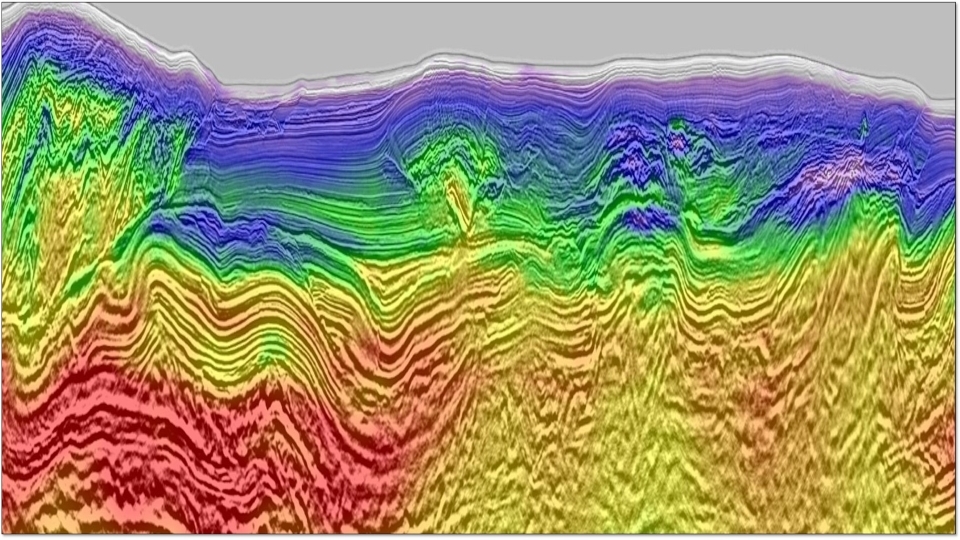
Back to Technical ContentWe present an efficient convex optimization strategy enabling the simultaneous attenuation of random and erratic noise with interpolation in pre-stack seismic data. For a particular analysis window, frequency slice spatial data can be reorganized into a block Toeplitz matrix with Toeplitz blocks in the spirit of Cadzow / Singular Spectrum Analysis (SSA) methods. The signal and erratic noise are respectively modeled as low-rank and sparse components of this matrix, then a Joint Low-Rank and Sparse Inversion (JLRSI) enables us to recover the low-rank signal component from noisy and incomplete data thanks to a joint minimization of a nuclear norm term and a L1 norm term. The convex optimization framework, related to recent developments in the field of compressed sensing, enables the formulation of a well-posed problem as well as the use of state-of-the-art algorithms. We suggest here an Alternating Directions Method of Multipliers (ADMM) scheme associated to an efficient singular value thresholding kernel. Numerical results on field data illustrate the effectiveness of the JLRSI approach at recovering missing data and increasing the signal-to-noise ratio.
Download Resource 
Publications
GeophysicsAuthors
Raphael Sternfels, Ghislain Viguier, Regis Gondoin, David Le Meur